回溯算法——理论基础

前言

我在大概两年前就学习过回溯算法，但总是学了就忘，写了很多例题但一到自己写就抓瞎，本质上还是不理解，现在打算跟着代码随想录系统的重新学一遍，记录一下自己的理解

递归for循环

回溯算法的本质就是穷举，但它比嵌套for更适用的一点是它可以实现任意k层的for循环，想象一下这个情境，输入一个参数k，实现k层嵌套循环。直接硬编码k层for循环是无法实现的，因为k是一个变化的参数，但是这个问题使用回溯就可以解决（准确地说是递归+for循环）

我们先来写一个两层的for循环

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        // ......
    }
}

实际上它的穷举结果可以抽象成一棵树，如下图所示

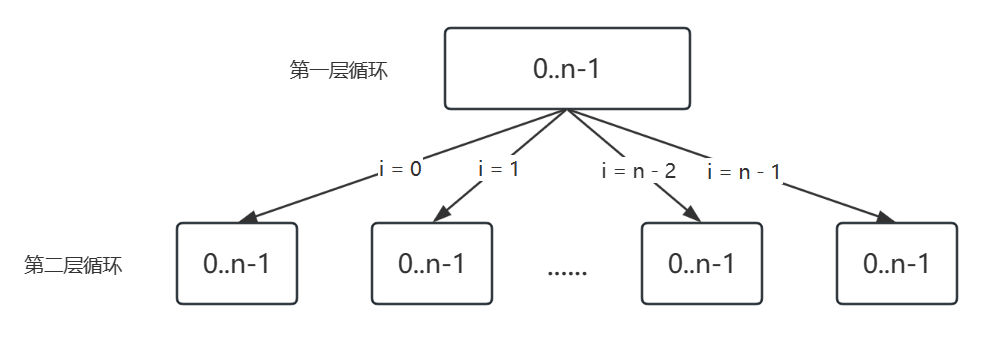
那么我们怎么使用递归+for循环实现这个穷举树呢，先给出代码

void trace(int layer) {
    if (layer == 2) {
        return;
    }
    for (int i = 0; i < n; i++) {
        // ...
        trace(layer + 1);
    }
}

使用一个参数layer表示当前循环的层数，当layer == 2时，退出递归，这也被称为递归的终止条件。每一层包含一个for循环，递归到第二层，也就是执行了两层for循环

乍一看，怎么使用递归反而更加复杂了，还多需要一个参数，但当我需要执行k层循环时，使用递归就变得轻而易举，而一般嵌套for循环就无法实现了

void trace(int layer, int k) {
    // 将递归层数用参数k表示
    if (layer == k) {
        return;
    }
    for (int i = 0; i < n; i++) {
        // ...
        trace(layer + 1, k);
    }
}

有了递归+for循环这一利器，我们就可以实现嵌套for循环无法实现的穷举了

我们再来看一下trace函数和穷举树的关系，我们在trace函数中使用参数k表示穷举树的深度，在每个节点中，for循环的穷举范围就是该节点的所有子状态，也称为宽度。在之后的解题中，分析出树的深度和宽度对我们写程序有很大的帮助，包括在剪枝中，也是围绕着宽度来分析

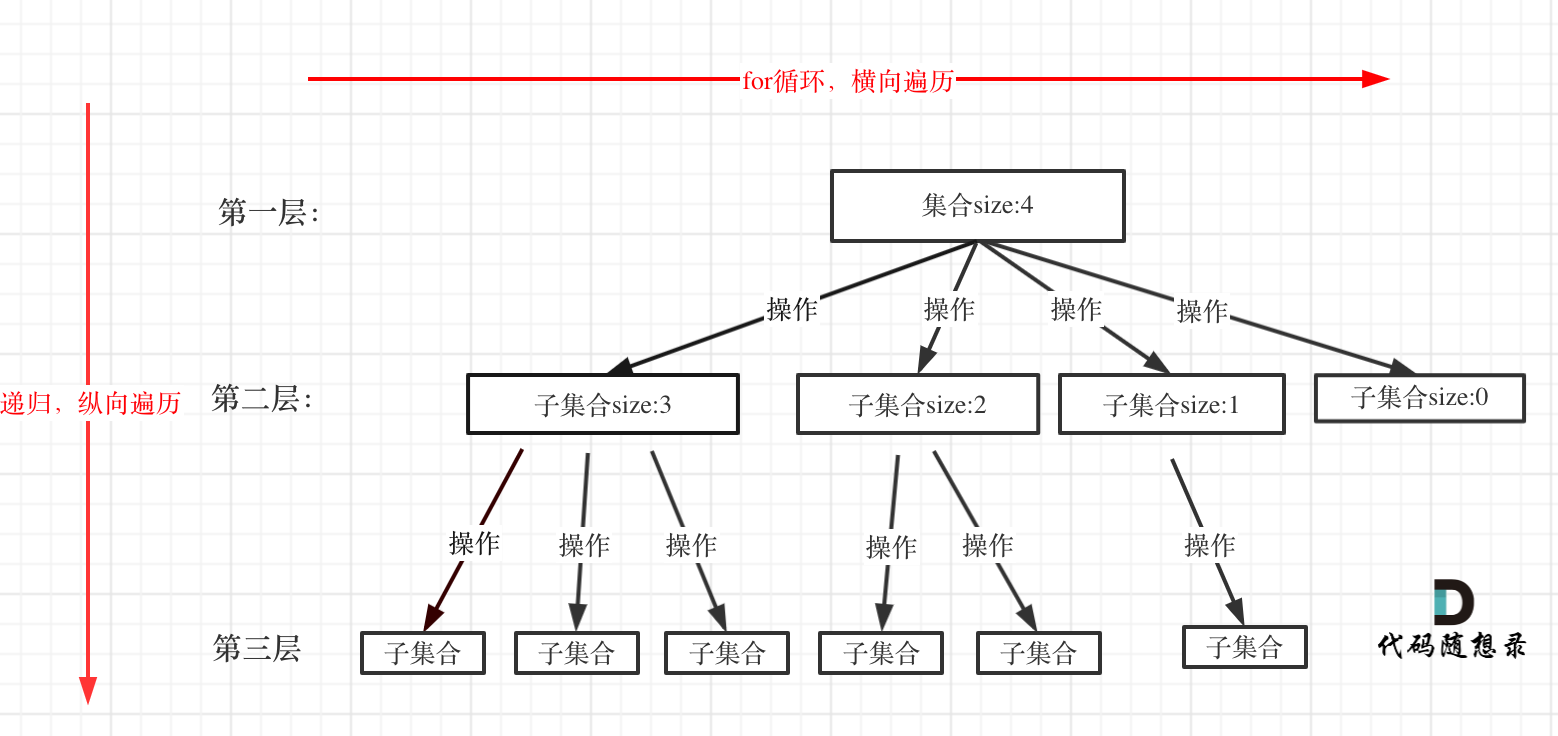
回溯算法

在上述框架下，我们得出回溯算法的模板

void backtrack(参数、状态) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtrack(路径，选择列表); // 递归
        回溯，撤销处理结果  // 回溯
    }
}

回溯算法之所以称为回溯算法，就是因为撤销处理结果这一步，那么为什么要撤销呢，实际上，回溯算法解决的问题通常要求给出所有符合要求的状态，倘若没有回溯这一步，一次穷举到达叶节点后，就无法继续穷举了，因此要撤回叶节点的结果，返回到上一层节点才能继续遍历其他节点

回溯算法可以解决以下问题

• 组合情况
• 分割集合
• 子集
• 全排列
• N皇后、解数独