K短路算法
前言
在大二做树数据结构课设时,选到的题目是做一个校园地图导航应用,其中需要实现一个寻路算法,并且有一个功能需要展示到达一个地点的多种路线方案,最终采用了K短路算法,在此记录一下
为了说明方便,文中用Python来实现代码
堆优化Dijkstra算法
Dijkstra算法是解决最短路径问题的经典算法,通过逐步扩展已知的最短路径集来找到最短路径,每次从未处理的顶点中选择一个距离源顶点最近的顶点,更新其邻居的最短路径值,直到所有顶点都处理完毕
在选择距离源顶点最近的顶点这一步上,可以使用最小堆来优化,算法的时间复杂度可以降到$O(n\log n)$
首先定义一个状态类,存储顶点和当前最短距离的状态
1
2
3
4
5
6
7
8
class Entry:
def __init__(self, vertex, dist):
self.vertex = vertex
self.dist = dist
# 比较当前最短距离,用于最小堆比较
def __lt__(self, other):
return self.dist < other.dist
使用heapq模块实现最小堆操作,堆优化的Dijkstra算法实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# size:顶点个数
# source:源点
# graph:带权无向图,邻接矩阵
visited = [False] * size # 各顶点的访问状态
dists = [inf] * size # 源点到各顶点的最短距离
heap = [] # 最小堆
# 初始状态
dists[source] = 0
cur_v = source
heapq.heappush(heap, Entry(cur_v, 0))
while len(heap) != 0:
cur_v = heapq.heappop(heap).vertex
visited[cur_v] = True
# 当前顶点的邻接点
adjoins = [adjoin for adjoin in range(size)
if adjoin != cur_v and graph[cur_v][adjoin] != inf]
# 遍历邻接点
for adjoin in adjoins:
# 若邻接点未访问过
if not visited[adjoin]:
# 源点到当前顶点的最短距离 + 当前顶点到邻接点的距离 < 源点到邻接点的最短距离
if dists[cur_v] + graph[cur_v][adjoin] < dists[adjoin]:
# 更新源点到邻接点的最短距离
dists[adjoin] = dists[cur_v] + graph[cur_v][adjoin]
heapq.heappush(heap, Entry(adjoin, dists[adjoin]))
运行测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
graph = [
[0, 2, inf, 6, inf],
[2, 0, 3, 8, 5],
[inf, 3, 0, inf, 7],
[6, 8, inf, 0, 9],
[inf, 5, 7, 9, 0]
]
size = len(graph)
source = 0
dists = Dijkstra(graph, size, source)
print(f'dists = {dists}')
# 运行结果
# dists = [0, 2, 5, 6, 7]
# 顶点0到顶点1的最短距离为2
# 顶点0到顶点2的最短距离为5
# 顶点0到顶点3的最短距离为6
# 顶点0到顶点4的最短距离为7
A*算法
A*算法定义了一个对当前状态的估价函数$f(x)=g(x)+h(x)$,其中$g(x)$为从初始状态到达当前状态的实际代价,$h(x)$为从当前状态到达目标状态的最佳路径的估计代价,$f(x)$为当前状态的代价值
应用在最短路径问题中,在Dijkstra算法中选择距离源顶点最近的顶点这一步上,对应到A*算法,就变成了选择代价值$f(x)$最小的顶点,这依然可以使用最小堆来实现
A*算法的关键在于估计代价$h(x)$的实现,$h(x)$也被称为启发式函数,$h(x)$计算的估计代价越精确,得到的最短路径越优,但同时越精确的代价计算消耗的时间越多,因此在$h(x)$的实现上需要权衡精确性和速度
同时,$h(x)$代价值的大小也会影响总代价值$f(x)$
- $h(x)$过小或等于0,A*算法退化为Dijkstra算法
- $h(x)$过大,A*算法退化为BFS算法
在导航应用中,可知某个地点的经纬度,可以看做一个网格地图,在网格地图中,有以下几种启发式函数
- 曼哈顿距离:$h(v)=\lvert v_x-goal_x\rvert+\lvert v_y-goal_y\rvert$
- 欧几里得距离:$h(v)=\sqrt{(v_x-goal_x)^2+(v_y-goal_y)^2}$
- 切比雪夫距离:$h(v)=\max(\lvert v_x-goal_x\rvert ,\lvert v_y-goal_y\rvert)$
使用欧几里得距离来实现A*算法如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# h函数实现欧几里得距离
def h(v, goal):
return sqrt((v[0] - goal[0]) ** 2 + (v[1] - goal[1]) ** 2)
def a_star(graph, size, position, source, goal):
visited = [False] * size # 各顶点的访问状态
dists = [inf] * size # 源点到各顶点的最短距离
heap = [] # 最小堆
back_from = {} # 记录回溯路径
# 初始状态
dists[source] = 0
cur_v = source
heapq.heappush(heap, Entry(cur_v, 0))
while len(heap) != 0:
cur_v = heapq.heappop(heap).vertex
visited[cur_v] = True
# 到达目标顶点停止
if cur_v == goal:
break
# 当前顶点的邻接点
adjoins = [adjoin for adjoin in range(size)
if adjoin != cur_v and graph[cur_v][adjoin] != inf]
# 遍历邻接点
for adjoin in adjoins:
# 若邻接点未访问过
if not visited[adjoin]:
# 源点到当前顶点的最短距离 + 当前顶点到邻接点的距离 < 源点到邻接点的最短距离
if dists[cur_v] + graph[cur_v][adjoin] < dists[adjoin]:
# 记录回溯路径
back_from[adjoin] = cur_v
# 更新源点到邻接点的最短距离
dists[adjoin] = dists[cur_v] + graph[cur_v][adjoin]
# 计算代价
cost = dists[adjoin] + h(position[adjoin], position[goal])
heapq.heappush(heap, Entry(adjoin, cost))
# 回溯路径
path = []
cur_v = goal
while cur_v in back_from:
path.append(cur_v)
cur_v = back_from[cur_v]
path.append(cur_v)
path.reverse()
return path, dists[goal]
运行测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
graph = [
[0, 2, inf, 6, inf],
[2, 0, 3, 8, 5],
[inf, 3, 0, inf, 7],
[6, 8, inf, 0, 9],
[inf, 5, 7, 9, 0]
]
size = len(graph)
source = 0
goal = 4
position = [(0, 0), (2, 0), (2, 2), (0, 3), (3, 3)]
path, dist = a_star(graph, size, position, source, goal)
print(f'path = {path}\ndist = {dist}')
# 运行结果
# path = [0, 1, 4]
# dist = 7
# 最短路径为0->1->4,距离为7
关于A*算法的更多介绍,可参考:Amit’s A* Pages
K短路算法
A*算法中每次选取的都是代价最小的顶点,这个选取就是一种取最短的最优化,当选取的顶点第一次为目标顶点时,第一条最短的路径就到达了目标顶点,那么推广一下,求第k条最短路径,也就需要选取的顶点第k次为目标顶点
我们可以将visited数组保存的内容变为到达顶点的次数,每次到达一个顶点i,令visited[i] += 1,当到达的顶点为目标顶点且到达次数为k时,跳出循环
此外,还有两个要注意的问题
对于
visited[i] > k的顶点,不应该继续遍历它们的邻接点因为当
visited[i] > k时,表示已经访问了该顶点k次,那么在产生的k条最短路径中一定都经过了该顶点,也就是经过该顶点产生了k条合法的最短路径,那么该顶点的邻接点状态就不必放入最小堆中进行比较,优化了运行效率,同时,这样也可以避免当图中出现环时,算法困在环中在将邻接点状态放入最小堆时,邻接点状态应包含邻接点的前驱顶点(也就是当前顶点)
这是在无向图或非简单有向图中会出现的问题,当遍历邻接点状态时,在无向图中会将当前顶点的前驱顶点也作为邻接点,将它的状态放入最小堆中,这可能会导致算法不停地在当前顶点和前驱顶点间跳转,陷入死循环
在Dijkstra算法或A*算法中,我们通过
visited数组来判断顶点是否被访问过,在遍历邻接点状态时,将未访问过的邻接点状态放入最小堆中,这样就过滤掉了前驱顶点,因为前驱顶点必然被访问过在K短路算法中,我们使用
visited数组来记录顶点的访问次数,仅仅通过访问次数难以过滤掉前驱顶点,因此在将邻接点状态放入最小堆时,应该将当前顶点作为前驱顶点添加到状态中。在遍历下一个顶点的邻接点时,就可以通过判断邻接点是否是该顶点的前驱顶点来过滤掉前驱顶点
修改状态类,增加代价、前驱顶点信息
1
2
3
4
5
6
7
8
9
class Entry:
def __init__(self, vertex, dist, cost, pre_entry=None):
self.vertex = vertex
self.dist = dist # 实际距离
self.cost = cost # 加上h(x)的代价值
self.pre_entry = pre_entry # 前驱顶点
def __lt__(self, other):
return self.cost < other.cost
K短路算法实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def h(v, goal):
return sqrt((v[0] - goal[0]) ** 2 + (v[1] - goal[1]) ** 2)
def ksp(graph, size, position, source, goal, k):
visited = [0] * size # 各顶点的访问次数
heap = [] # 最小堆
# 初始状态
cur_entry = Entry(source, 0, 0)
heapq.heappush(heap, cur_entry)
while len(heap) != 0:
cur_entry = heapq.heappop(heap)
cur_v = cur_entry.vertex
pre_entry = cur_entry.pre_entry
# 增加访问次数
visited[cur_v] += 1
# 到达目标顶点停止
if cur_v == goal and visited[cur_v] == k:
break
# 访问次数大于k,跳过
if visited[cur_v] > k:
continue
# 当前顶点的邻接点
adjoins = [adjoin for adjoin in range(size)
if adjoin != cur_v and graph[cur_v][adjoin] != inf]
# 遍历邻接点
for adjoin in adjoins:
# 当邻接点不是前驱顶点
if pre_entry is None or pre_entry.vertex != adjoin:
# 计算代价
dist = cur_entry.dist + graph[cur_v][adjoin]
cost = dist + h(position[adjoin], position[goal])
heapq.heappush(heap, Entry(adjoin, dist, cost, cur_entry))
# 回溯路径
dist = cur_entry.dist
path = []
while cur_entry is not None:
path.append(cur_entry.vertex)
cur_entry = cur_entry.pre_entry
path.reverse()
return path, dist
运行测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
graph = [
[0, 2, inf, 6, inf],
[2, 0, 3, 8, 5],
[inf, 3, 0, inf, 7],
[6, 8, inf, 0, 9],
[inf, 5, 7, 9, 0]
]
size = len(graph)
source = 0
goal = 4
position = [(0, 0), (2, 0), (2, 2), (0, 3), (3, 3)]
for k in range(1, 9):
path, dist = ksp(graph, size, position, source, goal, k)
print(f'第{k}短路: ( path = {path}, dist = {dist} )')
# 运行结果
# 第1短路: ( path = [0, 1, 4], dist = 7 )
# 第2短路: ( path = [0, 1, 2, 4], dist = 12 )
# 第3短路: ( path = [0, 3, 4], dist = 15 )
# 第4短路: ( path = [0, 1, 3, 4], dist = 19 )
# 第5短路: ( path = [0, 3, 1, 4], dist = 19 )
# 第6短路: ( path = [0, 1, 4, 2, 1, 4], dist = 22 )
# 第7短路: ( path = [0, 1, 3, 0, 1, 4], dist = 23 )
# 第8短路: ( path = [0, 3, 1, 2, 4], dist = 24 )
算法应用
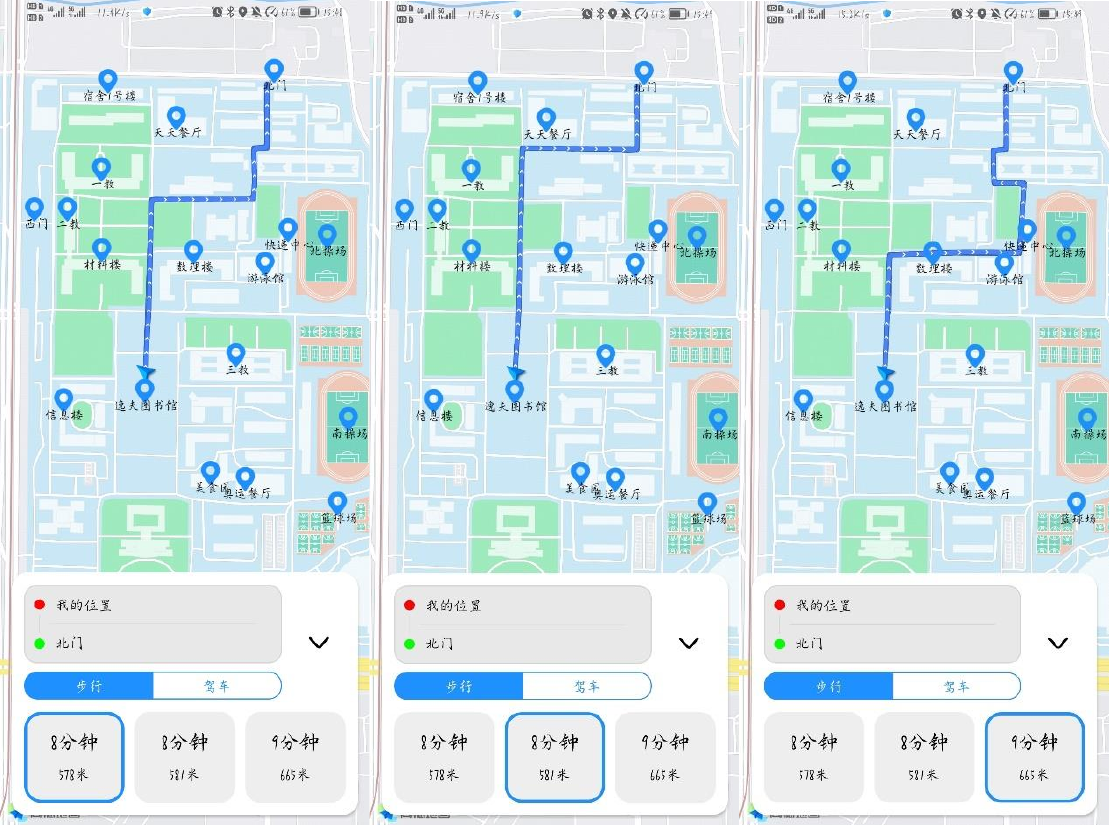
下面是当时实现的地图应用的截图,背景的地图使用的是高德的地图,地图上的地点以及路线均是通过K短路算法计算得到,再使用高德的API绘制在地图上
当前算法在一般情况下的运行效果不错,但当选定的两个地点过近时,计算得到的路径会有环(上面运行的示例结果中有包含环的结果),当前算法没有解决这一点,在应用中实现了一个过滤机制,若某条路径的路程大于等于最短路径路程的两倍,则去除该路径,经过该过滤机制,得出的路径结果已基本满足需求