《机器学习》——线性模型
基本形式
对样本$x=(x_1;x_2;x_3;…;x_d)$,有
\[f(x_i)=\omega^Tx+b\]其中$\omega=(\omega_1;\omega_2;…;\omega_d)$
线性回归
离散属性处理
- 具有序关系的属性可以连续化,如身高
- 不具有序关系的属性转化为k维向量
一元线性回归
对于一元线性回归
\[f(x_i)=\omega x_i+b\]使用均方误差来衡量$f(x)$与$y$的差别,并使其最小化来求解模型的方法称为最小二乘法
最小二乘参数估计
\[\begin{aligned} E(\omega,b)&=\sum\limits_{i=1}^m(f(x_i)-y_i)^2\\ \frac{\partial E(\omega,b)}{\partial \omega}&=2(\omega\sum\limits_{i=1}^mx_i^2-\sum\limits_{i=1}^m(y_i-b)x_i)\\ \frac{\partial E(\omega,b)}{\partial b}&=2(mb-\sum\limits_{i=1}^m(y_i-\omega x_i)) \end{aligned}\]令两个偏导为0可求得$\omega$和$b$最优解
多元线性回归
对于多元线性回归
\[f(x_i)=\omega^T x_i+b\]定义向量形式如下
\[\begin{aligned} X&=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1\\ x_{21} & x_{22} & \cdots & x_{2d} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ x_{m1} & x_{m2} & \cdots & x_{md} & 1\\ \end{bmatrix}=\begin{bmatrix} \vec{x}_1^T & 1\\ \vec{x}_2^T & 1\\ \vdots & \vdots\\ \vec{x}_m^T & 1\\ \end{bmatrix}\\ \hat{\omega}&=(\vec{\omega},b)\\ \vec{y}&=(y_1;y_2;...;y_m) \end{aligned}\]由最小二乘法有
\[\begin{aligned} E(\hat{\omega})&=(\vec{y}-X\hat{\omega})^T(\vec{y}-X\hat{\omega})\\ \frac{\partial E(\hat{\omega})}{\partial \omega}&=2X^T(X\hat{\omega}-\vec{y}) \end{aligned}\]当$X^TX$满秩时,令偏导为0有唯一解,也称为正规方程法
\[\hat\omega=(X^TX)^{-1}X^T\vec y\]当$X^TX$不满秩时,存在多组解,由算法的归纳偏好决定输出哪一组解,通常引入正则化项
广义线性模型
\[y=g^{-1}(\omega^Tx+b)\]其中函数$g(.)$单调可微,称为联系函数,可以理解为将线性模型的预测值与实际标记联系起来的函数
对数几率回归
对于二分类任务,使用线性模型需要将线性模型的输出值与分类联系起来
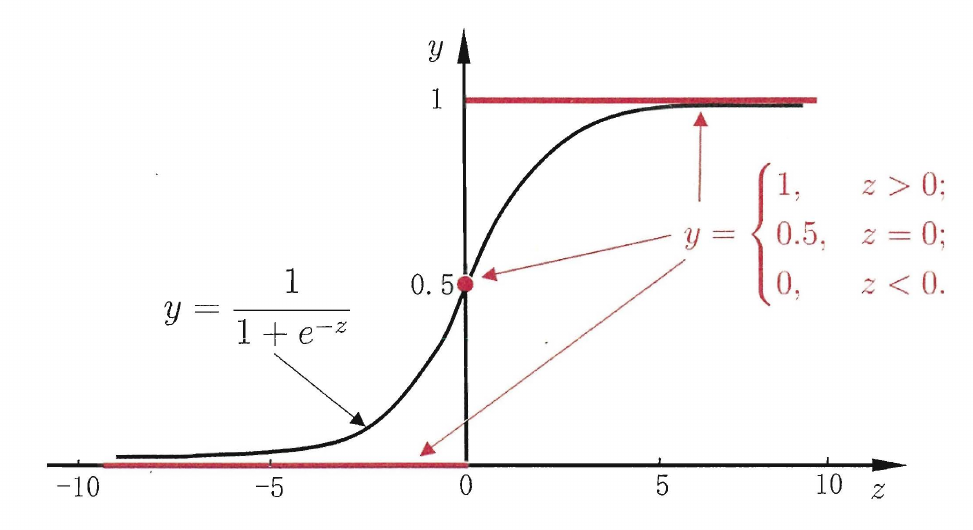
使用sigmoid函数作为联系函数
\[y=\frac{1}{1+e^{-z}}\]sigmoid函数将$(-\infty,+\infty)$映射到$(0,1)$之间
代入线性函数有
\[\begin{aligned} y&=\frac{1}{1+e^{-(\omega^Tx+b)}}\\ \ln\frac{y}{1-y}&=\omega^T+b \end{aligned}\]其中$\ln\frac{y}{1-y}$称为对数几率(logit),反映了正例的相对几率
将$y$重写为概率估计,通过极大似然估计可求解参数
\[\begin{aligned} p(y=1\vert x)&=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}}\\ p(y=0\vert x)&=\frac{1}{1+e^{\omega^Tx+b}} \end{aligned}\]线性判别分析
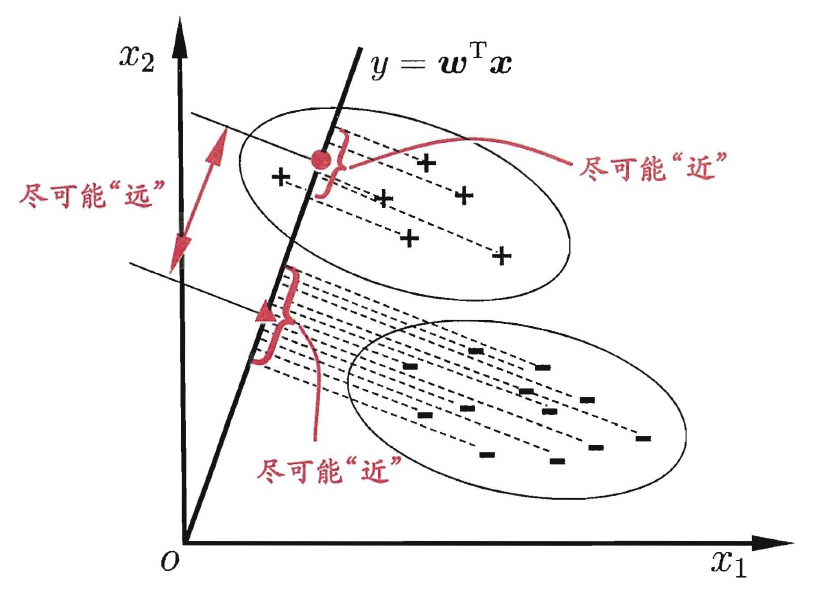
在二分类问题上,线性判别分析(LDA)通过将样本投影到一条直线上,同时使得相同类别的样本的投影点尽可能接近,而不同类别的样本的投影点尽可能远离,确定直线后,将新样本投影到该直线上,根据投影点的位置判定类别
LDA的目标是使同类样本的投影点尽可能接近,则可以使同类样本投影点的协方差尽可能小,使不同的样本的投影点尽可能远离,则可以使类中心的距离尽可能大,用$\mu_0$和$\mu_1$表示两类样本的均值向量,$\Sigma_0$和$\Sigma_1$表示两类样本的协方差矩阵,有最大化目标函数
\[J=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega}=\frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}\]多分类学习
对于多分类问题,通常是使用一些拆分策略,将其转换为多个二分类问题,通常有以下三种拆分策略
- 一对一(OvO):将N个类别两两配对,形成$N(N-1)/2$组二分类问题,最终结果取预测最多的类别
- 一对其余(OvR):将一个类别作为正例,其余类别作为反例,形成N个二分类问题
- 多对多(MvM):取多个类别作为正例,其他类别作为反例,通常使用纠错输出码(ECOC)拆分
ECOC分为两步
- 编码:对N个类别做M次划分,划分出M个训练集,训练出M个分类器
- 解码:M个分类器分别对测试样本分类,产生的预测标记组成一个编码,将这个编码与每个类别定义的编码进行比较,将其中距离最小的类别作为结果
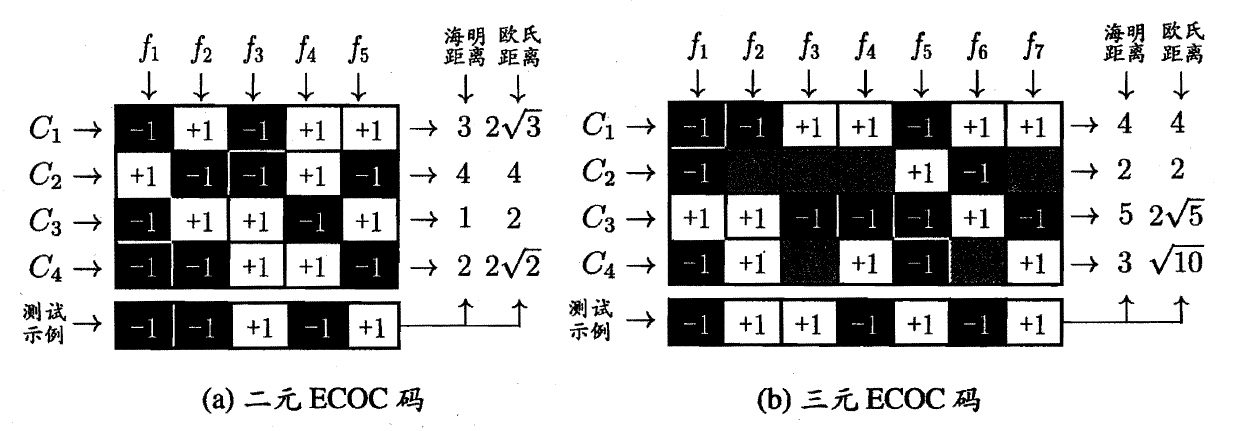
ECOC常见的有二元码和三元码,类别和类别划分组成编码矩阵,其中1表示正类,-1表示负类
a图中分类器f1的预测结果为$(-1,+1,-1,-1)$,f2的预测结果为$(+1,-1,+1,-1)$,f3的预测结果为$(-1,-1,+1,+1)$,f4的预测结果为$(+1,+1,-1,+1)$,f5的预测结果为$(+1,-1,+1,-1)$,对于C1类别组成了一个编码$(-1,+1,-1,+1,+1)$,使用该编码与测试样本的编码进行比较
对于同一个学习任务,一般编码越长,纠错能力越强,但编码越长,所需的分类器越多,训练开销越大
类别不平衡问题
类别不平衡是指分类任务重不同类别的训练样本数目差别很大,同时在使用OvR和MVM拆分多分类问题时也可能导致类别不平衡
使用再缩放策略解决类别不平衡问题
通常认为正反例的可能性相同,当正例几率大于0.5时预测为正例
\[\frac{y}{1-y}>1\]当正反例的数目不同时,假设训练集是真实样本集的无偏采样,当正例几率大于数据集中正例的观测几率就可以判为正例
\[\frac{y}{1-y}>\frac{m^+}{m^-}\]对预测值进行再缩放调整
\[\frac{y'}{1-y'}=\frac{y}{1-y}\times\frac{m^-}{m^+}\]实际操作中观测几率通常不能代表真实几率,此时使用三种方法处理
- 多数样本欠采样:删除多数样本
- 少数样本过采样:通常使用插值增加样本
- 阈值移动:将再缩放方法加入决策过程中