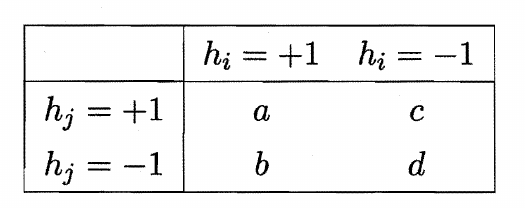《机器学习》——集成学习
个体与集成
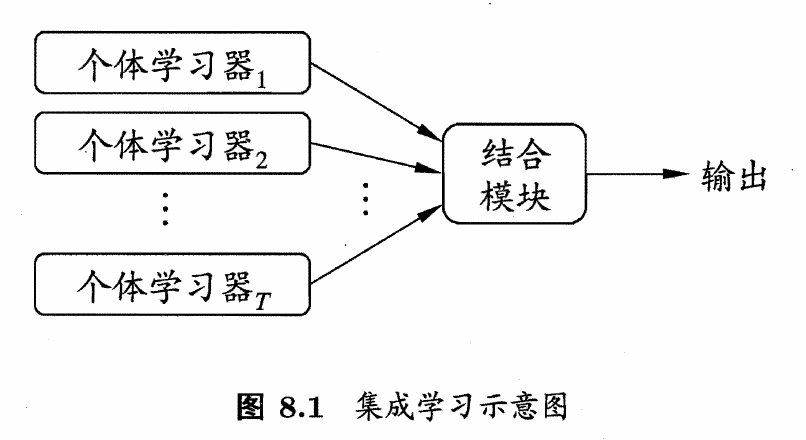
集成学习将多个个体学习器的学习结果通过某种策略结合起来,每个个体学习器可以使用相同的学习算法,称为基学习器,也可以使用不同的学习算法
集成学习通常针对弱学习器进行,个体学习器应该有一定的准确性和多样性,相互之间应该尽可能独立,这是集成学习研究的核心
集成学习方法可分为两类
- 序列化方法:个体学习器之间强依赖关系,必须串行生成,如Boosting
- 并行化方法:个体学习器之间不存在强依赖关系,可同时生成,如Bagging和随机森林
Boosting
Boosting是一类可将弱学习器提升到强学习器的算法,基本流程是先训练出一个基学习器,根据基学习器的表现对样本分布进行调整,使做错的样本收到更多关注,基于调整后的样本来训练下一个基学习器,直到训练出T个学习器,将T个学习器加权结合
Boosting算法中最著名的是AdaBoost算法
Boosting算法要求基学习器能对特定的数据分布进行学习,这可通过重赋权法实施,即在训练过程的每一轮中,根据样本分布为每个训练样本重新赋予一个权重
对无法接受带权样本的基学习算法,则可通过重采样法来处理,即在每一轮学习中,根据样本分布对训练集重新进行采样,再用重采样而得的样本集对基学习器进行训练
Bagging
Bagging基于自主采样法,对训练集进行m次有放回随机采样,产生一个采样集,采样出T个采样集,基于这些采样集训练出T个基学习器,再将基学习器进行结合,对于分类任务,通常使用简单投票法结合,对于回归任务,通常使用简单平均法结合
随机森林
在以决策树作为基学习器的Bagging算法的基础上,加入随机属性选择,形成了随机森林算法
一般决策树在属性集中直接选择一个最优属性进行划分,随机森林中首先随机选择出一个包含k个属性的属性集,在该属性集中选择最优属性进行划分,当$k=d$时,与一般决策树相同,当$k=1$时,则随机选择一个属性进行划分,一般情况下,设置$k=\log_2d$
结合策略
对于T个学习器的输出${h_1,h_2,…,h_T}$,有以下常见方法将它们结合起来
平均法
- 简单平均法:$H(x)={1\over T}\sum\limits_{i=1}^Th_i(x)$
- 加权平均法:$H(x)={1\over T}\sum\limits_{i=1}^T\omega_ih_i(x)$,通常要求$\sum\limits_{i=1}^T\omega_i=1,\omega_i\ge0$
简单平均法的性能未必弱于加权平均法,通常来说,个体学习器的性能相近时采用简单平均法,个体学习器的性能差距较大时采用加权平均法
投票法
对于一个学习器,它可能在多个类别上投票,输出表示为一个N维向量$(h_i^1(x);h_i^2(x);…;h_i^N(x))$
- 绝对多数投票法:若某个类别的投票数超过总票数一半,则预测为该类
- 相对多数投票法:预测为得票最多的类别,若有多个类别得票最高,则随机选择一个
- 加权投票法:对每个学习器的投票设置权重,预测为得票最多的类别
学习器的输出$h_i^j(x)$有以下两种,不同类型的输出不能混用
- 类标记:直接输出类别的标记值,称为硬投票
- 类概率:输出样本预测为某个类别的概率值,称为软投票
学习法
使用另一个学习器进行结合,典型代表有Stacking算法,Stacking算法中基学习器称为初级学习器,结合学习器称为次级学习器
Stacking算法先从初始训练集中训练出初始学习器,然后将所有初始学习器的输出作为次级学习器的输入,初始标记依然作为次级学习器的标记
当初级学习器输出为类概率,次级学习器使用多响应线性回归(MLR)时,效果较好
多样性
误差-分歧分解
误差-分歧分解公式,说明了个体学习器的准确性越高、多样性越大,集成性能越好
\[E=\bar E-\bar A\]其中$E$为集成泛化误差,$\bar E$为个体学习器的泛化误差的加权均值,$\bar A$为个体学习器的加权分歧值
分歧值表征了个体学习器在样本上的不一致性,反映了个体学习器的多样性
多样性度量
对于两个分类器,度量它们的多样性,典型做法是度量它们的相似度
设共有m个样本,构造两个分类器预测结果的列联表
不合度量:$dis_{ij}=\frac{b+c}{m}$,值越大,多样性越大
相关系数:$\rho_{ij}=\frac{ad-bc}{\sqrt{(a+c)(a+b)(c+d)(b+d)}}$
Q-统计量:$Q_{ij}=\frac{ad-bc}{ad+bc}$
$\kappa$-统计量:$\kappa=\frac{p_1-p_2}{1-p_2}$
$p_1$为结果一致的概率,$p_2$为结果偶然一致的概率,$p_1={a+d\over m},p_2={(a+b)(a+c)+(c+d)(b+d)\over m^2}$
多样性增强
多样性增强通常的做法是引入随机因素,对样本、输入属性、输出表示、参数进行扰动
- 样本扰动:基于采样法,对于不稳定的学习器有显著效果
- 输入属性扰动:每一个属性子集可以看做观察样本的不同视角,因此采用不同的属性子集可以训练出具有多样性的基学习器
- 输出表示扰动:对模型的输出表示进行处理,如随机改变一些样本的标记,或者对分类输出转化为回归输出
- 算法参数扰动:通过随机设置不同的参数训练出多样性较大的基学习器