监督与非监督学习
机器学习方法可以主要分为监督学习、非监督学习和半监督学习,而训练时使用的数据分为人工标注的有标签数据和无标签数据
-
监督学习
监督学习采用人工标注的有标签数据,将输入数据和对应的输出数据作为训练样本,通过训练模型来建立输入和输出之间的映射关系
-
无监督学习
无监督学习采用无标签数据,直接输入到模型中训练,让模型挖掘数据分布内在的模式,产生反映数据本身的统计规律或结构的特征
自监督学习:自监督学习是无监督学习的一种特殊形式,在中间设计辅助任务(如预测下一个词、填空等)来生成伪标签,使用伪标签与输入数据对模型进行有监督的训练,该方式生成的特征更侧重于能够通用地表示数据,从而可以将这些特征迁移到下游任务中
-
半监督学习
半监督学习结合了监督学习和无监督学习,利用少量的有标签数据和大量的无标签数据进行模型训练,提升模型的泛化能力
经验误差与过拟合
训练误差/经验误差:学习器在训练集上的误差
- 泛化误差:学习器在新样本上的误差
- 过拟合:学习器的学习能力过于强大,将样本的特点当做了一般性质
- 欠拟合:学习器的学习能力低下,没有学习到样本的一般性质
评估方法
使用一个测试集对学习器进行测试,产生的测试误差作为泛化误差的近似,从而评估学习器的泛化能力
对数据集划分出训练集和测试集的方法
-
留出法:直接将数据集划分为两个互斥的集合,划分要尽可能保持数据分布的一致性
单次使用留出法的结果往往不可靠,通常需要多次随机划分,然后取所有划分产生结果的平均值
-
交叉验证法:将数据集划分为 k 个互斥的集合,每轮用其中的 k-1 个集合作为训练集,剩下的 1 个集合作为测试集,产生 k 个结果,取其平均值
-
留一法:交叉验证法的特例,每个子集中只包含一个样本
-
自助法:对 m 个样本的数据集进行 m 次有放回随机抽样,产生的集合作为训练集,原始数据集作为测试集
机器学习中的参数分为两类
- 超参数:人工设定的参数
- 模型参数:模型学习中产生的参数
验证集:在训练集的基础上进一步划分为训练集和验证集,通过模型在验证集上的性能来评估模型和调参
性能度量
均方误差
回归任务中常用的性能度量是均方误差 MSE
错误率与精度
- 错误率:分类错误样本占总样本的比例
- 精度:分类正确的样本占总样本的比例
查准率与查全率
- 查准率:分类为正例中实际正例的比例,
- 查全率:分类正确的样本中实际正例的比例,
- PR 曲线:查准率为纵轴,查全率为横轴构成的曲线
通过 PR 曲线判断模型的性能
平衡点:查准率等于查全率的点的取值,当模型 A 的平衡点大于模型 B,可认为 A 性能优于 B
F1 分数:查准率与查全率的调和平均
F1 分数的一般形式
- 当 时,退化为 F1
- 当 时,查全率影响更大
- 当 时,查准率影响更大
当产生多个二分类混淆矩阵时,有两种做法
- macro:对每个混淆矩阵计算查准率和查全率,再取平均,得到 macro-P 和 macro-R,基于此,计算得到 macro-F1
- micro:对混淆矩阵的每个元素取平均,即计算 TP、FP、TN 和 FN 的平均值,基于此计算得到 micro-P 和 micro-R,进一步得到 micro-F1
ROC 与 AUC
将 TPR 作为纵轴,FPR 作为横轴构成 ROC 曲线,AUC 为 ROC 曲线下的面积
- TPR:真正例率,
- FPR:假正例率,
代价敏感错误率与代价曲线
对于不同类型的错误,可以为错误赋予非均等代价
总体代价敏感错误率
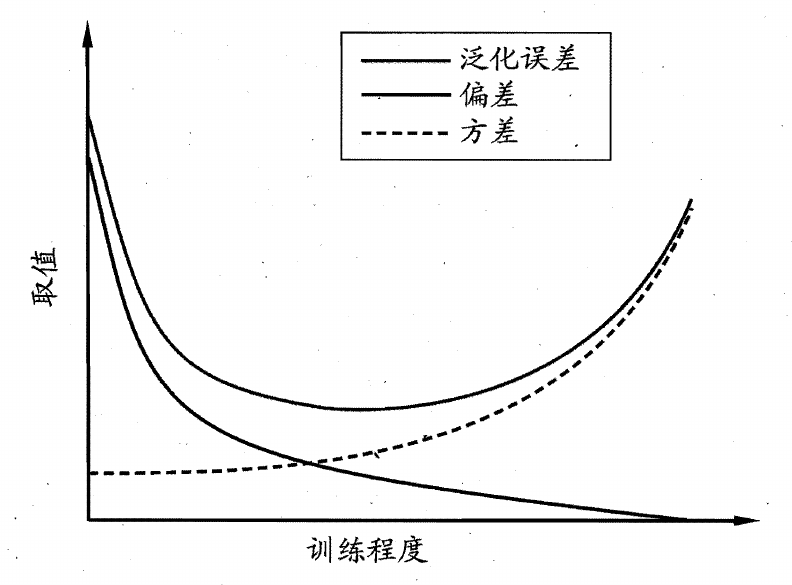
偏差与方差
偏差 - 方差分解可以用于解释泛化误差,泛化误差可理解为偏差、方差与噪声之和
- 偏差:表示了学习算法的期望预测与真实结果的偏离程度,表现了算法的拟合能力
- 方差:表示了训练集中数据的变动造成的学习性能变化
- 噪声:表示了当前任务上任何学习算法所能达到的期望泛化误差的下界,表现了学习问题本身的难度
偏差与方差随着算法拟合能力的变化而变化
- 当算法拟合能力不足时,期望预测与真实结果的偏离程度较大,而数据集中的数据变化不足以导致学习性能变化,此时偏差较大,方差较小
- 当算法拟合能力过强时,期望预测与真实结果的偏离程度较小,而数据集中的数据变化被学习器学习到,可能导致学习性能显著变化,此时偏差较小,方差较大