神经网络

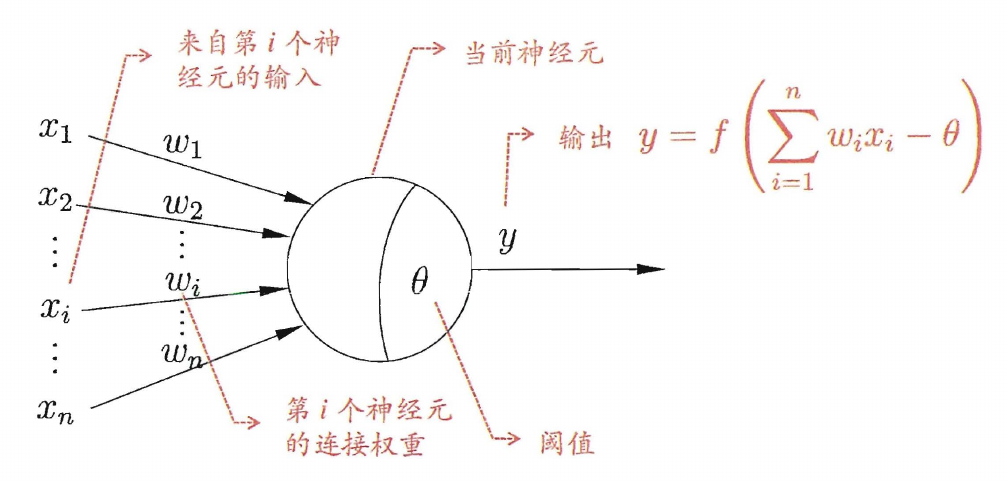
神经元模型

感知机与多层网络

感知机由两层神经元组成，包含输入层和输出层，只有输出层拥有激活函数

其中的权重和阈值可以通过学习得到，更一般地，将阈值看做一个固定输入为 -1 的哑节点的连接权重，权重和阈值的学习就统一为权重的学习

感知机的学习规则，设样本 $(\boldsymbol x,y)$，当前感知机的输出为 $\hat y$

$$\omega_i \leftarrow \omega_i+\Delta\omega_i\\ \Delta\omega=\eta(y-\hat y)x_i$$

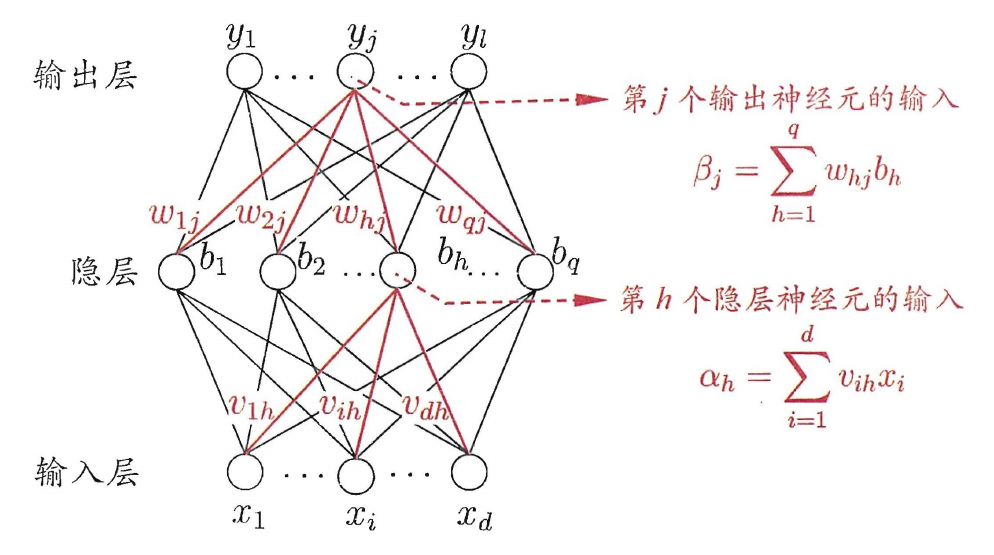
每层神经元与下一层神经元全互联，不存在跨层连接、同层连接，这样的网络称为多层前馈网络，其中隐层和输出层神经元具有激活函数，对输入进行加工

误差逆传播算法

误差逆传播算法 (BP) 可用于训练多层前馈网络，也可训练递归神经网络

除上图标记外，第 j 个输出神经元的阈值为 $\theta_j$，第 h 个隐层神经元的阈值为 $\gamma_h$

设训练样本 $(\boldsymbol x^k,y^k)$，网络输出为 $\hat y^k=(\hat y^k_1,\hat y^k_2,...,\hat y^k_l)$，隐层和输出层的激活函数均使用 sigmoid 函数

$$\hat y^k_j=f(\beta_j-\theta_j)$$

sigmoid 函数求导有

$$f'(x)=f(x)(1-f(x))$$

均方误差为

$$E_k={1\over2}\sum\limits_{j=1}^l(\hat y_j^k-y_j^k)^2$$

广义上的任意参数 $\nu$ 更新估计式为

$$\nu\leftarrow\nu+\Delta\nu$$

BP 算法使用梯度下降策略，以目标的负梯度方向对参数进行调整，给定学习率 $\eta$，计算输出层到隐层的权重 $\omega_{hj}$ 的梯度

$$\begin{aligned} \omega_{hj}&\leftarrow\omega_{hj}+\Delta\omega_{hj}\\ \Delta\omega_{hj}&=-\eta\frac{\partial E_k}{\partial\omega_{hj}}\\ \frac{\partial E_k}{\partial\omega_{hj}}&=\frac{\partial E_k}{\partial\hat y^k_j}\cdot\frac{\partial\hat y^k_j}{\partial\beta_j}\cdot\frac{\partial\beta_j}{\partial\omega_{hj}}\\ \frac{\partial\beta_j}{\partial\omega_{hj}}&=b_h\\ \frac{\partial E_k}{\partial\omega_{hj}}&=\frac{\partial E_k}{\partial\hat y^k_j}\cdot\frac{\partial\hat y^k_j}{\partial\beta_j}\cdot b_h\\ let\quad g_j&=-\frac{\partial E_k}{\partial\hat y^k_j}\cdot\frac{\partial\hat y^k_j}{\partial\beta_j}=-(\hat y^k_j-y^k_j)\hat y^k_j(1-\hat y^k_j)\\ Therefore,\quad \Delta\omega_{hj}&=\eta g_jb_h=\eta (y^k_j-\hat y^k_j)(\hat y^k_j-1)b_h \end{aligned}$$

$\theta_j$ 的梯度计算如下

$$\begin{aligned} \Delta\theta_j&=-\eta\frac{\partial E_k}{\partial\theta_j}\\ \frac{\partial E_k}{\partial\theta_j}&=\frac{\partial E_k}{\partial\hat y^k_j}\cdot\frac{\partial\hat y^k_j}{\partial\theta_j}=-(\hat y^k_j-y^k_j)\hat y^k_j(1-\hat y^k_j)=g_j\\ \Delta\theta_j&=-\eta g_j \end{aligned}$$

类似可得

$$\begin{aligned} e_h&=-\frac{\partial E_k}{\partial b_h}\cdot\frac{\partial b_h}{\partial \alpha_h}=b_h(1-b_h)\sum\limits^l_{j=1}\omega_{hj}g_j\\ \Delta\nu_{ih}&=\eta e_hx_i\\ \Delta\gamma_h&=-\eta e_h \end{aligned}$$

根据单个样本的误差来计算梯度并更新参数的 BP 算法称为标准 BP 算法，而使用整个数据集的累积误差 (误差平均值) 来更新参数的 BP 算法称为累积 BP 算法

• 累积 BP 算法：参数更新频率低，下降到一定程度后，下降非常缓慢
• 标准 BP 算法：参数更新频率高，更新效果可能会抵消，但在误差非常小时能够获得更优解

解决 BP 网络的过拟合问题

• 早停：使用训练集和验证集，当训练集误差降低而验证集误差升高时，立即停止训练
• 正则化：在损失函数中增加正则化项，描述了网络的复杂度，从而使网络偏好较小的权重，输出更加光滑

全局最小与局部最小

使用梯度下降的参数寻优方法时，总是沿负梯度方向搜索，即损失函数值下降最快的方向，在参数寻优的过程中，可能会陷入局部最小，若损失函数仅有一个局部最小，则为全局最小，若存在多个局部最小，有几种策略来跳出当前的局部最小

• 以多组初始值不同的参数来训练网络，即从不同的起点开始搜索，取其中误差最小的解
• 模拟退火算法：在搜索的每一步有概率接收比当前解更差的结果，使得搜索跳出局部最小
• 随机梯度下降：计算梯度时加入随机因素，使得在局部最小的梯度仍可能不为 0，从而跳出局部最小