《机器学习》：线性模型

基本形式

对样本 $x=(x_1;x_2;x_3;...;x_d)$ ，有

f(x_i)=\omega^Tx+b

其中 $\omega=(\omega_1;\omega_2;...;\omega_d)$

线性回归

离散属性处理

具有序关系的属性可以连续化，如身高
不具有序关系的属性转化为 k 维向量

一元线性回归

对于一元线性回归

f(x_i)=\omega x_i+b

使用均方误差来衡量 $f(x)$ 与 $y$ 的差别，并使其最小化来求解模型的方法称为最小二乘法

最小二乘参数估计

\begin{aligned} E(\omega,b)&=\sum\limits_{i=1}^m(f(x_i)-y_i)^2\\ \frac{\partial E(\omega,b)}{\partial \omega}&=2(\omega\sum\limits_{i=1}^mx_i^2-\sum\limits_{i=1}^m(y_i-b)x_i)\\ \frac{\partial E(\omega,b)}{\partial b}&=2(mb-\sum\limits_{i=1}^m(y_i-\omega x_i)) \end{aligned}

令两个偏导为 0 可求得 $\omega$ 和 $b$ 最优解

多元线性回归

对于多元线性回归

f(x_i)=\omega^T x_i+b

定义向量形式如下

\begin{aligned} X&=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1\\ x_{21} & x_{22} & \cdots & x_{2d} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ x_{m1} & x_{m2} & \cdots & x_{md} & 1\\ \end{bmatrix}=\begin{bmatrix} \vec{x}_1^T & 1\\ \vec{x}_2^T & 1\\ \vdots & \vdots\\ \vec{x}_m^T & 1\\ \end{bmatrix}\\ \hat{\omega}&=(\vec{\omega},b)\\ \vec{y}&=(y_1;y_2;...;y_m) \end{aligned}

由最小二乘法有

\begin{aligned} E(\hat{\omega})&=(\vec{y}-X\hat{\omega})^T(\vec{y}-X\hat{\omega})\\ \frac{\partial E(\hat{\omega})}{\partial \omega}&=2X^T(X\hat{\omega}-\vec{y}) \end{aligned}

当 $X^TX$ 满秩时，令偏导为 0 有唯一解，也称为正规方程法

\hat\omega=(X^TX)^{-1}X^T\vec y

当 $X^TX$ 不满秩时，存在多组解，由算法的归纳偏好决定输出哪一组解，通常引入正则化项

广义线性模型

y=g^{-1}(\omega^Tx+b)

其中函数 $g(.)$ 单调可微，称为联系函数，可以理解为将线性模型的预测值与实际标记联系起来的函数

对数几率回归

对于二分类任务，使用线性模型需要将线性模型的输出值与分类联系起来

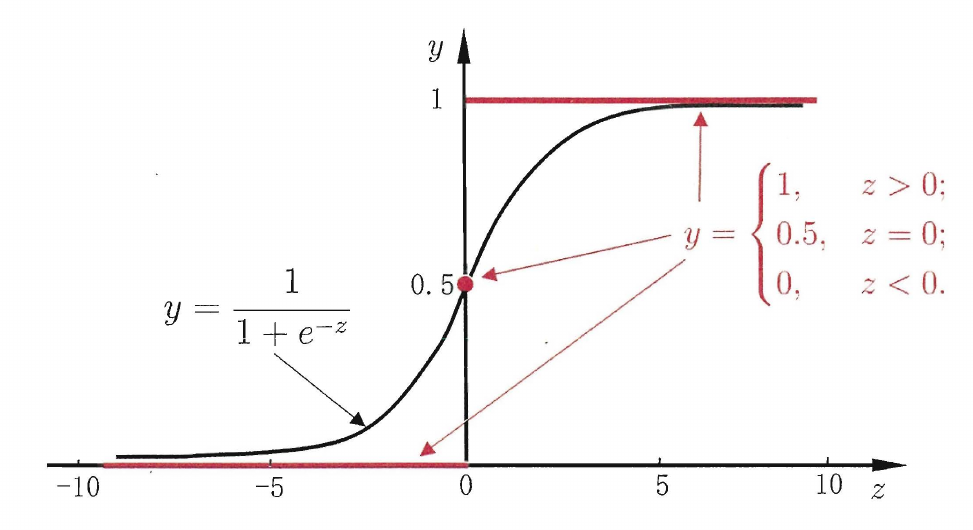
使用 sigmoid 函数作为联系函数

y=\frac{1}{1+e^{-z}}

sigmoid 函数将 $(-\infty,+\infty)$ 映射到 $(0,1)$ 之间

代入线性函数有

\begin{aligned} y&=\frac{1}{1+e^{-(\omega^Tx+b)}}\\ \ln\frac{y}{1-y}&=\omega^T+b \end{aligned}

其中 $\ln\frac{y}{1-y}$ 称为对数几率（logit），反映了正例的相对几率

将 $y$ 重写为概率估计，通过极大似然估计可求解参数

\begin{aligned} p(y=1\vert x)&=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}}\\ p(y=0\vert x)&=\frac{1}{1+e^{\omega^Tx+b}} \end{aligned}

线性判别分析

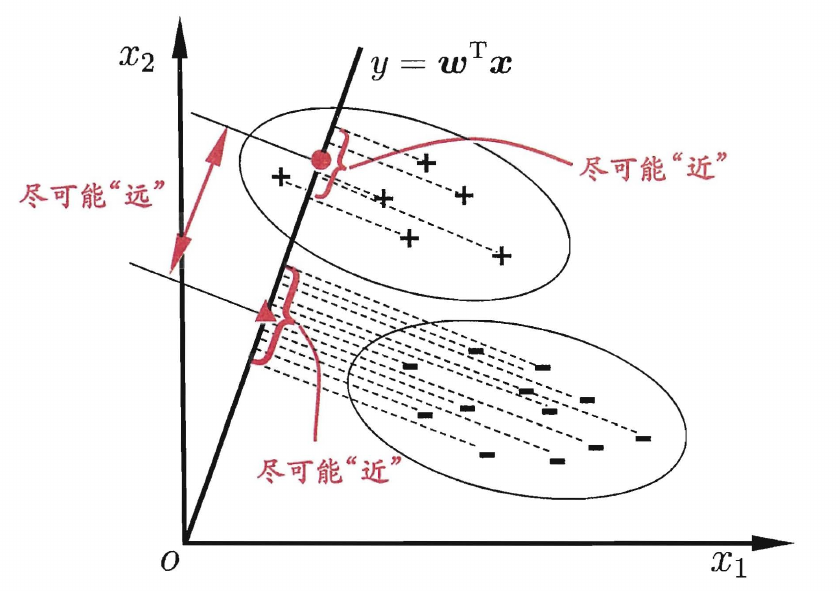
在二分类问题上，线性判别分析（LDA）通过将样本投影到一条直线上，同时使得相同类别的样本的投影点尽可能接近，而不同类别的样本的投影点尽可能远离，确定直线后，将新样本投影到该直线上，根据投影点的位置判定类别

LDA 的目标是使同类样本的投影点尽可能接近，则可以使同类样本投影点的协方差尽可能小，使不同的样本的投影点尽可能远离，则可以使类中心的距离尽可能大，用 $\mu_0$ 和 $\mu_1$ 表示两类样本的均值向量， $\Sigma_0$ 和 $\Sigma_1$ 表示两类样本的协方差矩阵，有最大化目标函数

J=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega}=\frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}

多分类学习

对于多分类问题，通常是使用一些拆分策略，将其转换为多个二分类问题，通常有以下三种拆分策略

一对一（OvO）：将 N 个类别两两配对，形成 $N(N-1)/2$ 组二分类问题，最终结果取预测最多的类别
一对其余（OvR）：将一个类别作为正例，其余类别作为反例，形成 N 个二分类问题
多对多（MvM）：取多个类别作为正例，其他类别作为反例，通常使用纠错输出码（ECOC）拆分

ECOC 分为两步

编码：对 N 个类别做 M 次划分，划分出 M 个训练集，训练出 M 个分类器
解码：M 个分类器分别对测试样本分类，产生的预测标记组成一个编码，将这个编码与每个类别定义的编码进行比较，将其中距离最小的类别作为结果

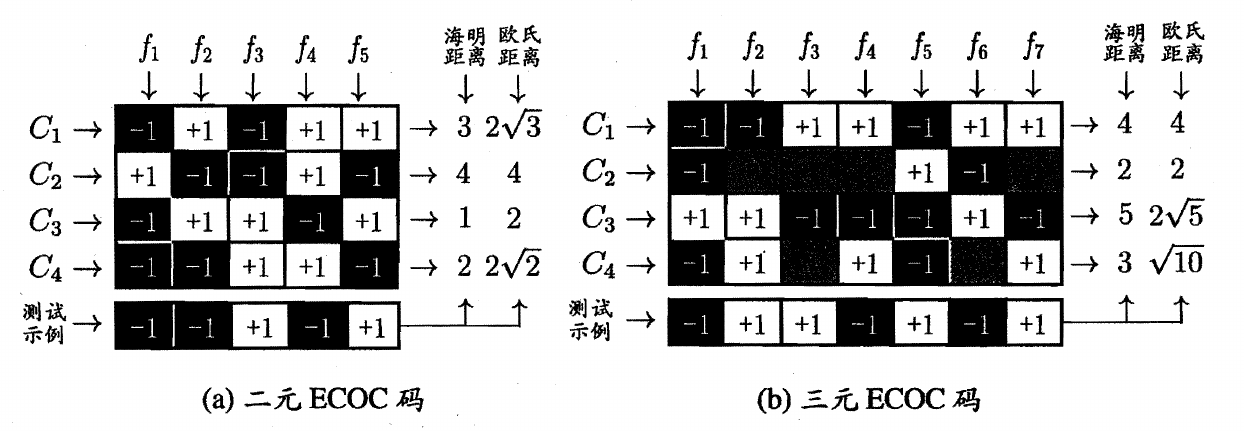
ECOC 常见的有二元码和三元码，类别和类别划分组成编码矩阵，其中 1 表示正类，-1 表示负类

a 图中分类器 f1 的预测结果为 $(-1,+1,-1,-1)$ ，f2 的预测结果为 $(+1,-1,+1,-1)$ ，f3 的预测结果为 $(-1,-1,+1,+1)$ ，f4 的预测结果为 $(+1,+1,-1,+1)$ ，f5 的预测结果为 $(+1,-1,+1,-1)$ ，对于 C1 类别组成了一个编码 $(-1,+1,-1,+1,+1)$ ，使用该编码与测试样本的编码进行比较